이번시간엔 gradient descent(경사 하강법)에 대해 알아보자
거의 대부분의 인공지능 관련 대학원이나 직무면접에서 단골로 등장하는 질문 중 하나가 바로 "gradient descent에 대해 설명해보세요~"이다.
그럴 때마다 우리는 대략 머릿속에 '경사 하강법이요!' 혹은 '인공지능이 최적화할 때 사용하는 알고리즘 중 하나예요~'처럼 추상적인 답변 그 이상은 머리에 떠오르지 않을 것이다.
그래서 이번 시간엔 이 gradient descent(경사 하강법)에 대해 보다 자세하고 쉽게 알아보고 넘어가려 한다.
📍 gradient descent란
gradient descent는 말 그대로 보면 gradient = 기울기, descent = 하강이라는 두 단어가 합쳐진 단어이다.
뜻 그대로를 이해하면 기울기가 하강한다(?) 정도로 인식될 것이다.
아직은 무슨 말인지 와 닫지 않는다. 나는 면접이나 누가 한마디로 설명해 달라고 하면 이와 같이 말할 거 같다.
"gradient descent는 한마디로 말하면, 주어진 함수에서 극소점을 찾기 위해 gradient가 최소가 되는 지점을 찾아가는 방법!이예요~"
여기서는 한마디로만 정의하고 아래쪽에서 구체적으로 알아보려 한다.
✅ gradient descent의 사용 이유
인공지능에서 gradient descent를 어떤 상황에 사용하는지 살펴보면 인공지능 에서의 Optimization(최적화)과 Loss function(cost function)의 개념부터 알고 있어야 한다. 왜냐하면 gradient descent는 인공지능이 최적화할 때 사용되는 알고리즘들 중 하나 이기 때문이다. 그리고 인공지능의 신경망은 파라미터를 더 좋은 값으로 개선하는 방향으로 학습해 나간다. 여기서 더 좋은 값을 결정하는 기준이 되는 것이 바로 손실함수 이기 때문에 우리는 이 둘에 대해 간략하게 짚고 넘어가자.
📌Optimization (최적화)
Optimization은 간단하게 말해 인공지능에서 신경망이 학습할 때 최적의 파라미터를 찾아가는 방식이라 정의할 수 있다.
모델의 예측값과 실제값의 차이를 우리는 오차라고 하며, 이 오차를 줄이기 위해 예측 값이 실제 값과 얼마나 유사한지 판단하는 기준이 필요한데 그것이 바로 손실 함수(loss function)이다.
📌Loss function(손실 함수)
앞서 설명한 예측값과 실제 값의 차이를 loss라고 이야기하며 이를 함수로 loss function으로 나타 낼 수 있는데, 우리는 이 loss function의 값을 줄이는 방향으로 학습을 진행한다.
손실 함수는 다양한 종류가 존재한다. 그중 회귀에 사용되는 손실 함수는 오차를 계산하는 방식에 따라 MAE, MSE, RMSE 등이 있으며 분류에 사용되는 손실 함수는 Bimary cross entropy나 Categorical cross entropy 등이 있다.
이 중 회귀에 가장 많이 사용되는 MSE(mean squared error)에 대해 하나만 설명해보겠다.
평균 제곱 오차(mean squared error)는 아래와 같이 오차 제곱의 합의 평균 형태이다.
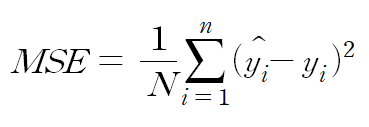
위 수식을 설명하면, ŷ 은 인공지능 모델이 예측한 값이며 y는 실제 값이다. 이 둘의 차이가 오차이고 제곱을 하는 이유는 오차 값이 음수이면 오차들을 더했을 때 오차의 절대적인 값이 적어져 정확한 오차의 총합을 알 수 없기에, 제곱을 한다. 그럼 여기서 절댓값을 취하면 된다고 할 수 있을 것이다.
실제로 절대값을 하는 방법은 MAE(mean absolute error)의 방법이 존재한다. 각각의 장단점이 존재하겠지만 절댓값이라는 연산이 모델 매개변수의 기울기 계산에 있어 단순 곱 연산에 비해 오랜 시간이 걸릴 것이며 제곱을 하게 됨으로 큰 오류가 강조된다. 따라서 실제로는 MSE가 더 자주 쓰인다.
이제 이 제곱을 취한 오류에 대해 모두 합쳐 평균을 낸다. 이게 대표적인 Loss function인 MSE이다.
이 손실 함수를 그래프로 보면 아래와 같이 표현된다.
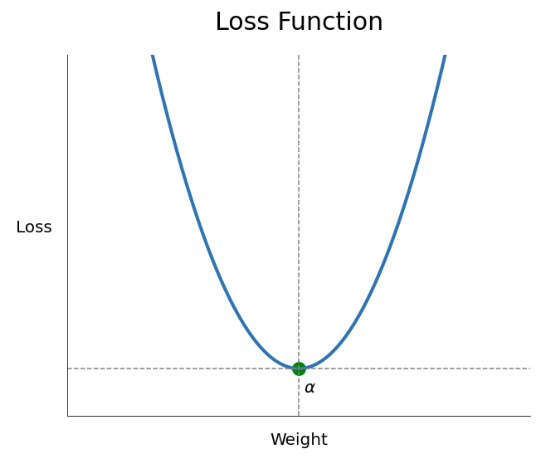
그렇다 보이는 그래프는 2차 함수의 형태이다.
여기서 손실 함수가 최소 값을 가지는 하나의 해는 α(알파)가 될 것이다. 최적화는 저 손실함수가 최적의 해 인 α(알파)를 찾아 나가는 과정이다.
(Optimization와 loss function에 대해 추후 더 자세히 포스팅할 예정)
여기서 위 그래프(loss function)의 극소값을 구할 때 가장 쉽게 생각할 수 있는 것이 미분 값이 0이 되는 지점을 찾으면 된다라고 머릿속에 떠오를 것이다.
하지만, 실제 고차원 데이터를 다룰 때 손실 함수의 그래프는 2차가 아닌 고차원 함수이다. (아래 그림 참고)
손실 함수 그래프가 위와 같을 때 쉽게 한 번에 최솟값을 찾기 힘들다. 그래서 최소값을 찾기 위해 최초 지점에서 조금씩 움직이며 찾아 나가며 최적의 값을 찾아야 하는 것이다.
이 방법들 중 하나가 Gradient descent 인 것이다.
✅ gradient descent
gradient descent는 등산을 할 때 정상에서 하산 할때에 많이 비유를 하곤 한다. 특히 우리가 앞이 보이지 않는 안개가 낀 산을 하산을 할때 모든 방향으로 더듬어 보며 비탈길의 경사가 가파른 방향으로 내려갈 것이다. (물론.. 위험 하지만 이론상!)
여기서 산 비탈길의 기울기가 그래프의 기울기로 보면 된다. 이 기울기가 감소하는 즉, gradient 가 descent 하는 방향으로 최적의 값을 찾는 방향으로 학습이 진행된다.
각 지점에서 gradient를 구하기 위해서는 각 점의 순간 변화량을 뜻하는 미분값을 알아야 한다.
📌gradient descent를 통한 최적화 과정
최적화를 하는 즉, 모델 가중치의 파라미터를 업데이트하는 과정에 대해 아래와 같이 설명할 수 있다.
1. 현재 지점의 gradient(기울기)를 구하여 이동할 방향을 정한다.
2. 한번 이동할때 마다 얼마나 이동 할 것인지 step size를 정하여 학습률(learning rate)을 곱해서 그만큼 이동한다
3. 최적의 해를 찾을 때까지 위의 과정을 반복한다
📌gradient descent 수식 유도
조금 더 구체적으로 수식을 통해 알아보자
2차 함수 그래프에서 최초 랜덤 위치에서 시작한다고 가정했을 때, 다음 지점은 어디로 가야 하는지에 대한 수식을 유도한다고 생각하고 보면 이해가 쉬울 것이다.
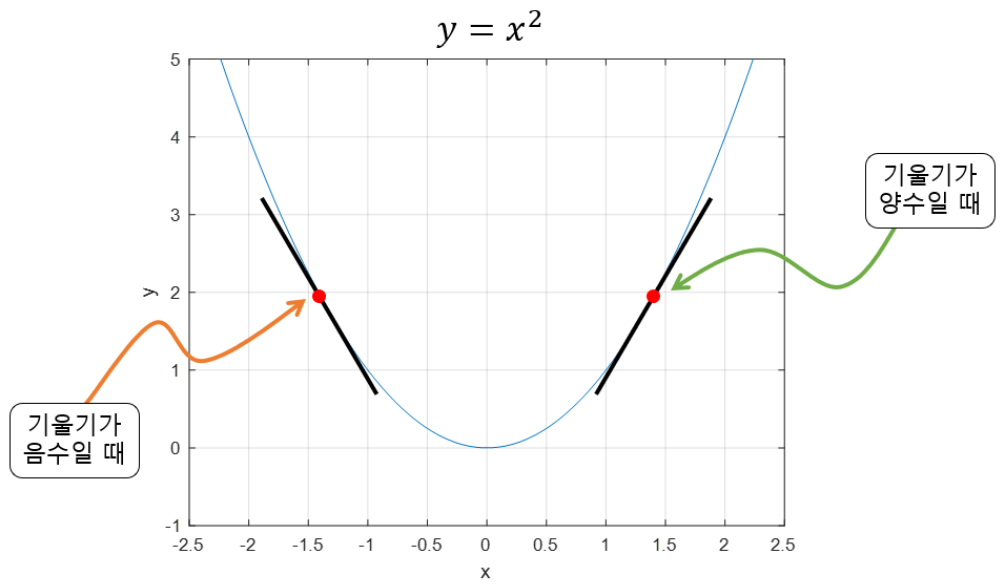
현재 지점에서 기울기를 먼저 구한 뒤 기울기가 양수인지 음수인지를 판단하고, 둘째로 얼마큼 이동할 것 인가(step size)를 정한 뒤 이동하면 이게 곧 gradient descent 수식이다.
위 그림에서 해당 지점의 기울기가 음수일 때는 양의 방향으로 , 양수일 경우는 음의 방향으로 이동하면 함수의 극소점을 찾을 수 있다. 그리고 얼마만큼 이동할 것인가에 대한 부분인 step size는
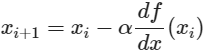
xᵢ번째 에서의 기울기에 α 인 step size를 곱하고 기울기의 부호의 반대로 움직임으로써 마이너스 기호를 사용하여 xᵢ 번째에서 xᵢ₊₁번째로 이동을 하는 것이다.
📌 learning rate(step size)
gradient descent에서는 적절한 learning rate가 필요하다. leaning rate는 step size(보폭)이라고도 하는데, 한 번에 얼마큼 이동할 것인가에 대한 부분이다.
이 부분은 상당히 중요한데 왜 그런지는 아래 이미지를 보고 이야기해보려 한다.
보다시피 작은 learning rate는 최적화되기까지 시간이 오래 걸린다. 그리고 global minimum을 못 찾을 수도 있다. 즉, local minimum에 빠질 수 있다는 것이다. (이 부분은 한계점에서 추가 설명)
그리고 너무 learning rate의 값이 크면 우측 그래프처럼 수렴이 아닌 발산을 해버린다.
이 때문에 항상 적절한 learning rate값을 찾는 것이 중요하다.
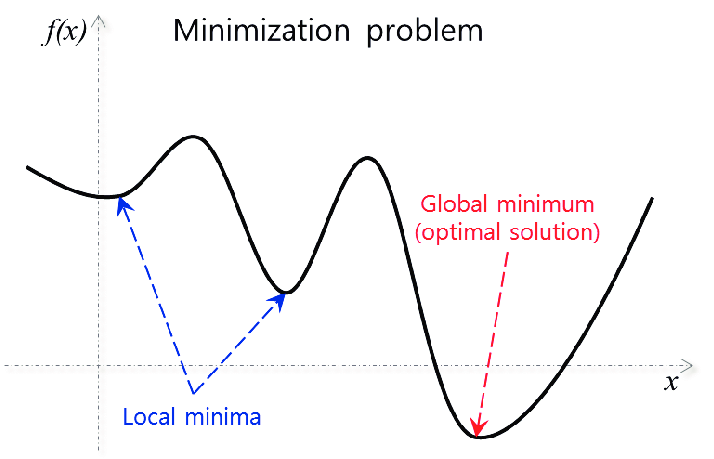
📌gradient descent의 한계점
gradient descent는 좋은 최적화 방법이지만 역시 한계점이 있다 바로 local minimua에 빠지기 쉬운 것이다.
위 이미지와 같이 global maximum을 나 두고 local minima에 빠지는 경우가 많다. 이때 local minima에서 탈출하기 위한 방법으로 momantum이나 stocastic gradient descent와 같은 여러 방법이 존재한다 이는 다음에 새로 포스팅을 통해 추가로 알아보겠다.


댓글